Syntax Tutorial
24 And the people murmured against Moses, saying, What shall we drink?
25 And he cried unto the Lord; and the Lord showed him a tree, which when he had cast into the waters, the waters were made sweet.
Exodus 15, 24-25
Moses supports models that have become known as hierarchical phrase-based models and syntax-based models. These models use a grammar consisting of SCFG (Synchronous Context-Free Grammar) rules. In the following, we refer to these models as tree-based models.
Content
Tree-Based Models
Traditional phrase-based models have as atomic translation step the mapping of an input phrase to an output phrase. Tree-based models operate on so-called grammar rules, which include variables in the mapping rules:
ne X1 pas -> not X1 (French-English)
ate X1 -> habe X1 gegessen (English-German)
X1 of the X2 -> le X2 X1 (English-French)
The variables in these grammar rules are called non-terminals, since their occurrence indicates that the process has not yet terminated to produce the final words (the terminals). Besides a generic non-terminal X, linguistically motivated non-terminals such as NP (noun phrase) or VP (verb phrase) may be used as well in a grammar (or translation rule set).
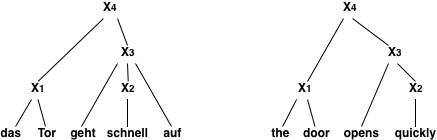
We call these models tree-based, because during the translation a data structure is created that is a called a tree. To fully make this point, consider the following input and translation rules:
Input: Das Tor geht schnell auf
Rules: Das Tor -> The door
schnell -> quickly
geht X1 auf -> opens X1
X1 X2 -> X1 X2
When applying these rules in the given order, we produce the translation The door opens quickly in the following fashion:
First the simple phrase mappings (1) Das Tor to The door and (2) schnell to quickly are carried out. This allows for the application of the more complex rule (3) geht X1 auf to opens X1. Note that at this point, the non-terminal X, which covers the input span over schnell is replaced by a known translation quickly. Finally, the glue rule (4) X1 X2 to X1 X2 combines the two fragments into a complete sentence.
Here is how the spans over the input words are getting filled in:
|4 ---- The door opens quickly ---- |
| |3 --- opens quickly --- |
|1 The door | |2 quickly | |
| Das | Tor | geht | schnell | auf |
Formally, such context-free grammars are more constraint than the formalism for phrase-based models. In practice, however, phrase-based models use a reordering limit, which leads to linear decoding time. For tree-based models, decoding is not linear with respect to sentence length, unless reordering limits are used.
Current research in tree-based models has the expectation to build translation models that more closely model the underlying linguistic structure of language, and its essential element: recursion. This is an active field of research.
A Word on Terminology
You may have read in the literature about hierarchical phrase-based, string-to-tree, tree-to-string, tree-to-tree, target-syntactified, syntax-augmented, syntax-directed, syntax-based, grammar-based, etc., models in statistical machine translation. What do the tree-based models support? All of the above.
The avalanche of terminology stems partly from the need of researchers to carve out their own niche, partly from the fact that work in this area has not yet fully settled on a agreed framework, but also from a fundamental difference. As we already pointed out, the motivation for tree-based models are linguistic theories and their syntax trees. So, when we build a data structure called a tree (as Computer Scientist call it), do we mean that we build a linguistic syntax tree (as Linguists call it)?
Not always, and hence the confusion. In all our examples above we used a single non-terminal X, so not many will claim the the result is a proper linguistic syntax with its noun phrases NP, verb phrases VP, and so on. To distinguish models that use proper linguistic syntax on the input side, on the output side, on both, or on neither all this terminology has been invented.
Let's decipher common terms found in the literature:
- hierarchical phrase-based: no linguistic syntax,
- string-to-tree: linguistic syntax only in output language,
- tree-to-string: linguistic syntax only in input language,
- tree-to-tree: linguistic syntax in both languages,
- target-syntactified: linguistic syntax only in output language,
- syntax-augmented: linguistic syntax only in output language,
- syntax-directed: linguistic syntax only in input language,
- syntax-based: unclear, we use it for models that have any linguistic syntax, and
- grammar-based: wait, what?
In this tutorial, we refer to un-annotated trees as trees, and to trees with syntactic annotation as syntax. So a so-called string-to-tree model is here called a target-syntax model.
Chart Decoding
Phrase-Based decoding generates a sentence from left to right, by adding phrases to the end of a partial translation. Tree-based decoding builds a chart, which consists of partial translation for all possible spans over the input sentence.
Currently Moses implements a CKY+ algorithm for arbitrary number of non-terminals per rule and an arbitrary number of types of non-terminals in the grammar.
Decoding
We assume that you have already installed the chart decoder, as described in the Get Started section.
You can find an example model for the decoder from the Moses web site. Unpack the tar ball and enter the directory sample-models:
% wget http://www.statmt.org/moses/download/sample-models.tgz
% tar xzf sample-models.tgz
% cd sample-models/string-to-tree
The decoder is called just as for phrase models:
% echo 'das ist ein haus' | moses_chart -f moses.ini > out
% cat out
this is a house
What happened here?
Trace
Using the option -T we can some insight how the translation was assembled:
41 X TOP -> <s> S </s> (1,1) [0..5] -3.593 <<0.000, -2.606, -9.711, 2.526>> 20
20 X S -> NP V NP (0,0) (1,1) (2,2) [1..4] -1.988 <<0.000, -1.737, -6.501, 2.526>> 3 5 11
3 X NP -> this [1..1] 0.486 <<0.000, -0.434, -1.330, 2.303>>
5 X V -> is [2..2] -1.267 <<0.000, -0.434, -2.533, 0.000>>
11 X NP -> DT NN (0,0) (1,1) [3..4] -2.698 <<0.000, -0.869, -5.396, 0.000>> 7 9
7 X DT -> a [3..3] -1.012 <<0.000, -0.434, -2.024, 0.000>>
9 X NN -> house [4..4] -2.887 <<0.000, -0.434, -5.774, 0.000>>
Each line represents a hypothesis that is part of the derivation of the best translation. The pieces of information in each line (with the first line as example) are:
- the hypothesis number, a sequential identifier (
41),
- the input non-terminal (
X),
- the output non-termial (
S),
- the rule used to generate this hypothesis (
TOP -> <s> S </s>),
- alignment information between input and output non-terminals in the rule (
(1,1)),
- the span covered by the hypothesis, as defined by input word positions (
[0..5]),
- the score of the hypothesis (
3.593),
- its component scores (
<<...>>):
- unknown word penalty (
0.000),
- word penalty (
-2.606),
- language model score (
-9.711),
- rule application probability (
2.526), and
- prior hypotheses, i.e. the children nodes in the tree, that this hypothesis is built on (
20).
As you can see, the model used here is a target-syntax model, It uses linguistic syntactic annotation on the target side, but on the input side everything is labeled X.
Rule Table
If we look at the string-to-tree directory, we find two files: the configuration file moses.ini which points to the language model (in lm/europarl.srilm.gz), and the rule table file rule-table.
The configuration file moses.ini has a fairly familiar format. It is mostly identical to the configuration file for phrase-based models. We will describe further below in detail the new parameters of the chart decoder.
The rule table rule-table is an extension of the Pharaoh/Moses phrase-table, so it will be familiar to anybody who has used it before. Here are some lines as example:
gibt [X] ||| gives [ADJ] ||| 1.0 ||| ||| 3 5
es gibt [X] ||| there is [ADJ] ||| 1.0 ||| ||| 2 3
[X][DT] [X][NN] [X] ||| [X][DT] [X][NN] [NP] ||| 1.0 ||| 0-0 1-1 ||| 2 4
[X][DT] [X][ADJ] [X][NN] [X] ||| [X][DT] [X][ADJ] [X][NN] [NP] ||| 1.0 ||| 0-0 1-1 2-2 ||| 5 6
[X][V] [X][NP] [X] ||| [X][V] [X][NP] [VP] ||| 1.0 ||| 0-0 1-1 ||| 4 3
Each line in the rule table describes one translation rule. It consists of five components separated by three bars:
- the source string and source left-hand-side,
- the target string and target left-hand-side,
- score(s): here only one, but typically multiple scores are used,
- the alignment between non-terminals (using word positions starting with 0, as source-target), and
- frequency counts of source & target phrase (for debugging purposes; not used during decoding).
The format is slightly different from the Hiero format. For example, the Hiero rule
[X] ||| [X,1] trace ' ||| [X,1] 추적 ' \
||| 0.727273 0.444625 1 0.172348 2.718
is formatted as
[X][X] trace ' [X] ||| [X][X] 추적 ' [X] \
||| 0.727273 0.444625 1 0.172348 2.718 ||| 0-0 ||| 2 3
A syntax rule in a string-to-tree grammar:
[NP] ||| all [NN,1] ||| 모든 [NN,1] \
||| 0.869565 0.627907 0.645161 0.243243 2.718
is formatted as
all [X][NN] [X] ||| 모든 [X][NN] [NP] \
||| 0.869565 0.627907 0.645161 0.243243 2.718 ||| 1-1 ||| 23 31
The format can also a represent a tree-to-string rule, which has no Hiero equivalent:
all [NN][X] [NP] ||| 모든 [NN][X] [X] \
||| 0.869565 0.627907 0.645161 0.243243 2.718 ||| 1-1 ||| 23 31
Usually, you will also need these 'glue' rules:
<s> [X][S] </s> [X] ||| <s> [X][S] </s> [TOP] ||| 1.0 ||| 1-1
<s> [X][NP] </s> [X] ||| <s> [X][NP] </s> [TOP] ||| 1.0 ||| 1-1
<s> [X] ||| <s> [S] ||| 1 |||
[X][S] </s> [X] ||| [X][S] </s> [S] ||| 1 ||| 0-0
[X][S] [X][X] [X] ||| [X][S] [X][X] [S] ||| 2.718 ||| 0-0 1-1
Finally, this rather technical rule applies only to spans that cover everything except the sentence boundary markers <s> and </s>. It completes a translation with of a sentence span (S).
More Example
The second rule in the table, that we just glanced at, allows something quite interesting: the translation of a non-contiguous phrase: macht X auf.
Let us try this with the decoder on an example sentence:
% echo 'er macht das tor auf' | moses_chart -f moses.ini -T trace-file ; cat trace-file
[...]
14 X TOP -> <s> S </s> (1,1) [0..6] -7.833 <<0.000, -2.606, -17.163, 1.496>> 13
13 X S -> NP VP (0,0) (1,1) [1..5] -6.367 <<0.000, -1.737, -14.229, 1.496>> 2 11
2 X NP -> he [1..1] -1.064 <<0.000, -0.434, -2.484, 0.357>>
11 X VP -> opens NP (1,1) [2..5] -5.627 <<0.000, -1.303, -12.394, 1.139>> 10
10 X NP -> DT NN (0,0) (1,1) [3..4] -3.154 <<0.000, -0.869, -7.224, 0.916>> 6 7
6 X DT -> the [3..3] 0.016 <<0.000, -0.434, -0.884, 0.916>>
7 X NN -> gate [4..4] -3.588 <<0.000, -0.434, -7.176, 0.000>>
he opens the gate
You see the creation application of the rule in the creation of hypothesis 11. It generates opens NP to cover the input span [2..5] by using hypothesis 10, which coveres the span [3..4].
Note that this rule allows us to do something that is not possible with a simple phrase-based model. Phrase-based models in Moses require that all phrases are contiguous, they can not have gaps.
The final example illustrates how reordering works in a tree-based model:
% echo 'ein haus ist das' | moses_chart -f moses.ini -T trace-file ; cat trace-file
41 X TOP -> <s> S </s> (1,1) [0..5] -2.900 <<0.000, -2.606, -9.711, 3.912>> 18
18 X S -> NP V NP (0,2) (1,1) (2,0) [1..4] -1.295 <<0.000, -1.737, -6.501, 3.912>> 11 5 8
11 X NP -> DT NN (0,0) (1,1) [1..2] -2.698 <<0.000, -0.869, -5.396, 0.000>> 2 4
2 X DT -> a [1..1] -1.012 <<0.000, -0.434, -2.024, 0.000>>
4 X NN -> house [2..2] -2.887 <<0.000, -0.434, -5.774, 0.000>>
5 X V -> is [3..3] -1.267 <<0.000, -0.434, -2.533, 0.000>>
8 X NP -> this [4..4] 0.486 <<0.000, -0.434, -1.330, 2.303>>
this is a house
The reordering in the sentence happens when hypothesis 18 is generated. The non-lexical rule S -> NP V NP takes the underlying children nodes in inverse order ((0,2) (1,1) (2,0)).
Not any arbitrary reordering is allowed --- as this can be the case in phrase models. Reordering has to be motivated by a translation rule. If the model uses real syntax, there has to be a syntactic justification for the reordering.
Decoder Parameters
The most important consideration in decoding is a speed/quality trade-off. If you want to win competitions, you want the best quality possible, even if it takes a week to translate 2000 sentences. If you want to provide an online service, you know that users get impatient, when they have to wait more than a second.
Beam Settings
The chart decoder has an implementation of CKY decoding using cube pruning. The latter means that only a fixed number of hypotheses are generated for each span. This number can be changed with the option cube-pruning-pop-limit (or short cbp). The default is 1000, higher numbers slow down the decoder, but may result in better quality.
Another setting that directly affects speed is the number of rules that are considered for each input left hand side. It can be set with ttable-limit.
Limiting Reordering
The number of spans that are filled during chart decoding is quadratic with respect to sentence length. But it gets worse. The number of spans that are combined into a span grows linear with sentence length for binary rules, quadratic for trinary rules, and so on. In short, long sentences become a problem. A drastic solution is the size of internal spans to a maximum number.
This sounds a bit extreme, but does make some sense for non-syntactic models. Reordering is limited in phrase-based models, and non-syntactic tree-based models (better known as hierarchical phrase-based models) and should limit reordering for the same reason: they are just not very good at long-distance reordering anyway.
The limit on span sizes can be set with max-chart-span. In fact its default is 10, which is not a useful setting for syntax models.
Handling Unknown Words
In a target-syntax model, unknown words that just copied verbatim into the output need to get a non-terminal label. In practice unknown words tend to be open class words, most likely names, nouns, or numbers. With the option unknown-lhs you can specify a file that contains pairs of non-terminal labels and their probability per line.
Optionally, we can also model the choice of non-terminal for unknown words through sparse features, and optimize their cost through MIRA or PRO. This is implemented by relaxing the label matching constraint during decoding to allow soft matches, and allowing unknown words to expand to any non-terminal. To activate this feature:
use-unknown-word-soft-matches = true (in EMS config)
-unknown-word-label FILE1 -unknown-word-soft-matches FILE2 (in train-model.perl)
Technical Settings
The parameter non-terminals is used to specify privileged non-terminals. These are used for unknown words (unless there is a unknown word label file) and to define the non-terminal label on the input side, when this is not specified.
Typically, we want to consider all possible rules that apply. However, with a large maximum phrase length, too many rule tables and no rule table limit, this may explode. The number of rules considered can be limited with rule-limit. Default is 5000.
Training
In short, training uses the identical training script as phrase-based models. When running train-model.perl, you will have to specify additional parameters, e.g. -hierarchical and -glue-grammar. You typically will also reduce the number of lexical items in the grammar with -max-phrase-length 5.
That's it.
Training Parameters
There are a number of additional decisions about the type of rules you may want to include in your model. This is typically a size / quality trade-off: Allowing more rule types increases the size of the rule table, but lead to better results. Bigger rule tables have a negative impact on memory use and speed of the decoder.
There are two parts to create a rule table: the extraction of rules and the scoring of rules. The first can be modified with the parameter --extract-options="..." of train-model.perl. The second with --score-options="...".
Here are the extract options:
--OnlyDirect: Only creates a model with direct conditional probabilities p(f|e) instead of the default direct and indirect (p(f|e) and p(e|f)).
--MaxSpan SIZE: maximum span size of the rule. Default is 15.
--MaxSymbolsSource SIZE and --MaxSymbolsTarget SIZE: While a rule may be extracted from a large span, much of it may be knocked out by sub-phrases that are substituted by non-terminals. So, fewer actual symbols (non-terminals and words remain). The default maximum number of symbols is 5 for the source side, and practically unlimited (999) for the target side.
--MinWords SIZE: minimum number of words in a rule. Default is 1, meaning that each rule has to have at least one word in it. If you want to allow non-lexical rules set this to zero. You will not want to do this for hierarchical models.
--AllowOnlyUnalignedWords: This is related to the above. A rule may have words in it, but these may be unaligned words that are not connected. By default, at least one aligned word is required. Using this option, this requirement is dropped.
--MaxNonTerm SIZE: the number of non-terminals on the right hand side of the rule. This has an effect on the arity of rules, in terms of non-terminals. Default is to generate only binary rules, so the setting is 2.
--MinHoleSource SIZE and --MinHoleTarget SIZE: When sub-phrases are replaced by non-terminals, we may require a minimum size for these sub-phrases. The default is 2 on the source side and 1 (no limit) on the target side.
--DisallowNonTermConsecTarget and --NonTermConsecSource. We may want to restrict if there can be neighboring non-terminals in rules. In hierarchical models there is a bad effect on decoding to allow neighboring non-terminals on the source side. The default is to disallow this -- it is allowed on the target side. These switches override the defaults.
--NoFractionalCounting: For any given source span, any number of rules can be generated. By default, fractional counts are assigned, so probability of these rules adds up to one. This option leads to the count of one for each rule.
--NoNonTermFirstWord: Disallows that a rule starts with a non-terminal.
Once rules are collected, the file of rules and their counts have to be converted into a probabilistic model. This is called rule scoring, and there are also some additional options:
--OnlyDirect: only estimates direct conditional probabilities. Note that this option needs to be specified for both rule extraction and rule scoring.
--NoLex: only includes rule-level conditional probabilities, not lexical scores.
--GoodTuring: Uses Good Turing discounting to reduce actual accounts. This is a good thing, use it.
Training Syntax Models
Training hierarchical phrase models, i.e., tree-based models without syntactic annotation, is pretty straight-forward. Adding syntactic labels to rules, either on the source side or the target side, is not much more complex. The main hurdle is to get the annotation. This requires a syntactic parser.
Syntactic annotation is provided by annotating all the training data (input or output side, or both) with syntactic labels. The format that is used for this uses XML markup. Here an example:
<tree label="NP"> <tree label="DET"> the </tree> \
<tree label="NN"> cat </tree> </tree>
So, constituents are surrounded by an opening and a closing <tree> tag, and the label is provided with the parameter label. The XML markup also allows for the placements of the tags in other positions, as long as a span parameter is provided:
<tree label="NP" span="0-1"/> <tree label="DET" span="0-0"/> \
<tree label="NN" span="1-1"/> the cat
After annotating the training data with syntactic information, you can simply run train-model.perl as before, except that the switches --source-syntax or --target-syntax (or both) have to be set.
You may also change some of the extraction settings, for instance --MaxSpan 999.
Annotation Wrappers
To obtain the syntactic annotation, you will likely use a third-party parser, which has its own idiosyncratic input and output format. You will need to write a wrapper script that converts it into the Moses format for syntax trees.
We provide wrappers (in scripts/training/wrapper) for the following parsers.
- Bitpar is available from the web site of the University of Munich. The wrapper is
parse-de-bitpar.perl
- Collins parser is availble from MIT. The wrapper is
parse-en-collins.perl
If you wrote your own wrapper for a publicly available parsers, please share it with us!
Relaxing Parses
The use of syntactic annotation puts severe constraints on the number of rules that can be extracted, since each non-terminal has to correspond to an actual non-terminal in the syntax tree.
Recent research has proposed a number of relaxations of this constraint. The program relax-parse (in training/phrase-extract) implements two kinds of parse relaxations: binarization and a method proposed under the label of syntax-augmented machine translation (SAMT) by Zollmann and Venugopal.
Readers familiar with the concept of binarizing grammars in parsing, be warned: We are talking here about modifying parse trees, which changes the power of the extracted grammar, not binarization as a optimization step during decoding.
The idea is the following: If the training data contains a subtree such as
then it is not possible to extract translation rules for Ariel Sharon without additional syntactic context. Recall that each rule has to match a syntactic constituent.
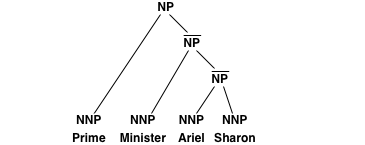
The idea of relaxing the parse trees is to add additional internal nodes that makes the extraction of additional rules possible. For instance left-binarization adds two additional nodes and converts the subtree into:
The additional node with the label ^NP allows for the straight-forward extraction of a translation rule (of course, unless the word alignment does not provide a consistent alignment).
The program relax-parse allows the following tree transformations:
--LeftBinarize and --RightBinarize: Adds internal nodes as in the example above. Right-binarization creates a right-branching tree.
--SAMT 1: Combines pairs of neighboring children nodes into tags, such as DET+ADJ. Also nodes for everything except the first child (NP\\DET) and everything except the last child (NP/NN) are added.
--SAMT 2: Combines any pairs of neighboring nodes, not only children nodes, e.g., VP+DET.
--SAMT 3: not implemented.
--SAMT 4: As above, but in addition each previously unlabeled node is labeled as FAIL, so no syntactic constraint on grammar constraint remains.
Note that you can also use both --LeftBinarize and --RightBinarize. Note that in this case, as with all the SAMT relaxations, the resulting annotation is not any more a tree, since there is not a single set of rule applications that generates the structure (now called a forest).
Here an example, what parse relaxation does to the number of rules extracted (English-German News Commentary, using Bitpar for German, no English syntax):
| Relaxation Setting | Number of Rules |
| no syntax | 59,079,493 |
| basic syntax | 2,291,400 |
| left-binarized | 2,914,348 |
| right-binarized | 2,979,830 |
| SAMT 1 | 8,669,942 |
| SAMT 2 | 35,164,756 |
| SAMT 4 | 131,889,855 |
On-Disk Rule Table
The rule table may become too big to fit into the RAM of the machine. Instead of loading the rules into memory, it is also possible to leave the rule table on disk, and retrieve rules on demand.
This is described in On-Disk Phrase Table.
Using Meta-symbols in Non-terminal Symbols (e.g., CCG)
Often a syntactic formalism will use symbols that are part of the meta-symbols that denote non-terminal boundaries in the SCFG rule table, and glue grammar. For example, in Combinatory Categorial Grammar (CCG, Steedman, 2000), it is customary to denote grammatical features by placing them after the non-terminal symbol inside square brackets, as in S[dcl] (declarative sentence) vs. S[q] (interrogative sentence).
Although such annotations may be useful to discriminate good translations from bad, including square brackets in the non-terminal symbols themselves can confuse Moses. Some users have reported that category symbols were mangled (by splitting them at the square brackets) after converting to an on-disk representation (and potentially in other scenarios -- this is currently an open issue). A way to side-step this issue is to escape square brackets with a symbol that is not part of the meta-language of the grammar files, e.g. using the underscore symbol:
S[dcl] => S_dcl_
and
S[q] => S_q_
before extracting a grammar. This should be done in all data or tables that mention such syntactic categories. If the rule table is automatically extracted, it suffices to escape the categories in the <tree label="..."...> mark-up that is supplied to the training script. If you roll your own rule tables (or use an unknown-lhs file), you should make sure they are properly escaped.
Different Kinds of Syntax Models
String-to-Tree
Most SCFG-based machine translation decoders at the current time are designed to uses hierarchical phrase-based grammar (Chiang, 2005) or syntactic grammar. Joshua, cdec, Jane are some of the open-sourced systems that have such decoders.
The hierarchical phrase-based grammar is well described elsewhere so we will not go into details here. Briefly, the non-terminals are not labelled with any linguistically-motivated labels. By convention, non-terminals have been simply labelled as X, e.g.
X --> der X1 ||| the X1
Usually, a set of glue rules are needed to ensure that the decoder always output an answer. By convention, the non-terminals for glue rules are labelled as S, e.g.
S --> <s> ||| <s>
S --> X1 </s> ||| X1 </s>
S --> X1 X2 ||| X1 X2
In a syntactic model, non-terminals are labelled with linguistically-motivated labels such as 'NOUN', 'VERB' etc. For example:
DET --> der ||| the
ADJ --> kleines ||| small
These labels are typically obtained by parsing the target side of the training corpus. (However, it is also possible to use parses of the source side which has been projected onto the target side (Ambati and Chen, 2007) ).
The input to the decoder when using this model is a conventional string, as in phrase-based and hierarchical phrase-based models. The output is a string. However, the CFG-tree derivation of the output (target) can also be obtained (in Moses by using the -T argument), the non-terminals in this tree will be labelled with the linguistically-motivated labels.
For these reasons, these syntactic models are called 'target' syntax models, or 'string-to-tree' model, by many in the Moses community and elsewhere. (Some papers by people at ISI inverted this naming convention due to their adherance to the noisy-channel framework).
The implementation of string-to-tree models is fairly standard and similar across different open-source decoders such as Moses, Joshua, cdec and Jane.
There is a 'string-to-tree' model among the downloadable sample models.
The input to the model is the string:
das ist ein kleines haus
The output string is
this is a small house
The target tree it produces is
(TOP <s> (S (NP this) (VP (V is) (NP (DT a) (ADJ small) (NN house)))) </s>)
RECAP - The input is a string, the output is a tree with linguistically-motivated labels.
Tree-to-string
Unlike the string-to-tree model, the tree-to-string model is not as standardized across different decoders. This section describes the Moses implementation.
Input tree representation
The input to the decoder is a parse tree, not a string. For Moses, the parse tree should be formatted using XML. The decoder converts the parse tree into an annotated string (a chart?). Each span in the chart is labelled with the non-terminal from the parse tree. For example, the input
<tree label="NP"> <tree label="DET"> the </tree> <tree label="NN"> cat </tree> </tree>
is converted to an annotated string
the cat
-DET- -NN--
----NP-----
To support easier glue rules, the non-terminal 'X' is also added for every span in the annotated string. Therefore, the input above is actually converted to:
the cat
-DET- -NN--
--X-- --X--
----NP-----
-----X-----
Translation rules
During decoding, the non-terminal of the rule that spans a substring in the sentence must match the label on the annoated string. For example, the following rules can be applied to the above sentence.
NP --> the katze ||| die katze
NP --> the NN1 ||| der NN1
NP --> DET1 cat ||| DET1 katze
NP --> DET1 NN2 ||| DET1 NN2
However, these rules can't as they don't match one or more non-terminals.
VB --> the katze ||| die katze
NP --> the ADJ1 ||| der ADJ1
NP --> ADJ1 cat ||| ADJ1 katze
ADV --> ADJ1 NN2 ||| ADJ1 NN2
Therefore, non-terminal in the translation rules in a tree-to-string model acts as constraints on which rules can be applied. This constraint is in addition to the usual role of non-terminals.
A feature which is currently unique to the Moses decoder is the ability to separate out these two roles. Each non-terminal in all translation rules is represented by two labels:
- The source non-terminal which constrains rules to the input parse tree
- The target non-terminal which has the normal parsing role.
When we need to differentiate source and target non-terminals, the translation rules are instead written like this:
NP --> the NN1 ||| X --> der X1
This rule indicates that the non-terminal should span a NN constituent in the input text, and that the whole rule should span an NP constituent. The target non-terminals in this rule are both X, therefore, this rule would be considered part of tree-to-string grammar.
(Using this notation is probably wrong as the source sentence is not properly parsed - see next section. It may be better to express the Moses tree-to-string grammar as a hierarchical grammar, with added constraints. For example:
X --> the X1 ||| der X1 ||| LHS = NP, X_1 = NN
However, this may be even more confusing so we will stick with our convention for now.)
RECAP - Grammar rules in Moses have 2 labels for each non-terminals; one to constrain the non-terminal to the input parse tree, the other is used in parsing.
Consequences
1. The Moses decoder always checks the source non-terminal, even when it is decoding with a string-to-string or string-to-tree grammar. For example, when checking whether the following rule can be applied
X --> der X1 ||| the X1
the decoder will check whether the RHS non-terminal, and the whole rule, spans an input parse constituent X.
Therefore, even when decoding with a string-to-string or string-to-tree grammar, it is necessary to add the X non-terminal to every input span. For example, the input string the cat must be annotated as follows
the cat
--X-- --X--
-----X-----
to allow the string to be decoded with a string-to-string or string-to-tree grammar.
2. There is no difference between a linguistically derived non-terminal label, such as NP, VP etc, and the non-linguistically motivated X label. They can both be used in one grammar, or even 1 translation rule. This 'mixed-syntax' model was explored in (Hoang and Koehn, 2010) and in Hieu Hoang's thesis
3. The source non-terminals in translation rules are used just to constrain against the input parse tree, not for parsing. For example, if the input parse tree is
(VP (NP (PRO he)) (VB goes))
and tree-to-string rules are:
PRO --> he ||| X --> il
VB --> goes ||| X --> va
VP --> NP1 VB2 ||| X --> X1 X2
This will create a valid translation. However, the span over the word 'he' will be labelled as PRO by the first rule, and NP by the 3rd rule.
This is illustrated in more detail in Hieu's thesis Section 4.2.11.
4. To avoid the above and ensure that source spans are always consistently labelled, simply project the non-terminal label to both source and target. For example, change the rule
VP --> NP1 VB2 ||| X --> X1 X2
to
VP --> NP1 VB2 ||| VP --> NP1 VB2
Format of text rule table
The format of the Moses rule table is different from that used by Hiero, Joshua and cdec, and has often been a source of confusion. We shall attempt to explain the reasons in this section.
The format is derived from the Pharaoh/Moses phrase-based format. In this format, a translation rule
a b c --> d e f , with word alignments a1, a2 ..., and probabilities p1, p2, ...
is formatted as
a b c ||| d e f ||| p1 p2 ... ||| a1 a2 ...
For a hierarchical pb rule,
X --> a X1 b c X2 ||| d e f X2 X1
The Hiero/Joshua/cdec format is
X ||| a [X,1] b c [X,2] ||| d e f [X,2] [X,1] ||| p1 p2 ...
The Moses format is
a [X][X] b c [X][X] [X] ||| d e f [X][X] [X][X] [X] ||| p1 p2 ... ||| 1-4 4-3
For a string-to-tree rule,
VP --> a X1 b c X2 ||| d e f NP2 ADJ1
the Moses format is
a [X][ADJ] b c [X][NP] [X] ||| d e f [X][NP] [X][ADJ] [VP] ||| p1 p2 ... ||| 1-4 4-3
For a tree-to-string rule,
VP --> a ADJ1 b c NP2 ||| X --> d e f X2 X1
The Moses format is
a [ADJ][X] b c [NP][X] [VP] ||| d e f [NP][X] [ADJ][X] [X] ||| p1 p2 ... ||| 1-4 4-3
The main reasons for the difference between the Hiero/Joshua/cdec and Moses formats are as follows:
- The text rule table should be easy to convert to a binary, on-disk format. We have seen in the community that this allows much larger models to be used during decoding, even on memory-limited servers. To make the conversion efficient, the text rule table must have the following properties:
- For every rule, the sequence of terminals and non-terminals in the first column (the 'source' column) should match the lookup sequence that the decoder will perform.
- The file can be sorted so that the first column is in alphabetical order. The decoder needs to look up the target non-terminals on the right-hand-side of each rule so the first column consists of source terminals and non-terminal, and target non-terminals from the right-hand-side.
- The phrase probability calculations should be performed efficiently. To calculate p(t | s) = count(t,s) / count(s) the extract file must be sorted in contiguous order so that each count can be performed and used to calculate the probability, then discarded immediately to save memory. Similarly for p(s | t) = count(t,s) / count(t)
The Hiero/Joshua/cdec file format is sufficient for hierarchical models, but not for the various syntax models supported by Moses.


 Language Models
Language Models
 Tuning
Tuning
 Sparse features
Sparse features